Merge Path - A Visually Intuitive Approach to Parallel Merging 论文解读

Publish on: Classify at:
Words:2547 Read:≈ 6min Views: Comments:

在看DuckDB技术博客时，了解到这篇论文。文章提出的算法非常实用，在工程实践中应用效果也很好。本文主要对论文核心部分进行解读，并会根据自己的理解加以叙述，若有不当之处，欢迎纠正。

介绍

在工程实践中，合并两个有序数组是非常常见的操作。最直观的实现方式就是采用一次归并排序，直接将两个有序数组合并生成一个新的有序数组。这种方式简单直观，也最容易实现，在数据集比较小的时候，性能特别好，时延几乎不计。但是在数据集较大的情况下，对于数据库这种对时延较为苛刻的系统来说，时延则不得不成为一个关注点。

在现代CPU多核架构下，可以充分利用CPU并行计算能力，采用多线程并行合并可以成倍提升性能，降低时延。

给一个长度为 \(n\) 的乱序数组，将其排序，考虑merge-sort算法，需要 \(\log_2n\) 轮排序，第一轮排序需要将 \(n/2\) 个 \(pairs\) 比较排序，第二轮需要将 \(n/4\) 个 \(pairs\) 排序，最后一轮将 \(2\) 个 \(pairs\) 排序生成单独的排序数组。

考虑使用并行merge-sort算法，使用 \(p\) 核计算机，假设 \(n \gg p\)，在前面的轮次，每个核可以负责一批 \(pairs\) 的排序工作，越往后需要排序的 \(pairs\) 更少，那么并不是每个核都能分得 \(pairs\)，不能充分发挥并行化计算能力。为了有效地发挥并行计算能力，需要对有序数组的合并也并行化，这样每个核在任何时候都能参与计算。

论文认为一个高效的并行合并算法必须具备如下特征：

  • 所有核拥有相同的工作量（负载均衡）
  • 尽可能少的核间通信
  • 最小化额外工作（为了并行化所做的额外工作）
  • 高效内存访问（高缓存命中率和最小的缓存一致性开销）

一种简单的方法是将两个有序数组按照核数平均切割成多个子数组，然后每个核分配一对长度相同的子数组，各个核排序生成一个有序数组，再将所有有序数组串联起来便得到最终的排序数组。如下：

arr1 = [1,3,5,7,9,11,13,15,17]   split to --> [1,3,5]        [7,9,11]        [13,15,17]
arr2 = [2,4,6,8,10,12,14,16,18]  split to --> [2,4,6]        [8,10,12]       [14,16,18]
                                            core0|          core1|           core2|
                                           [1,2,3,4,5,6,  7,8,9,10,11,12,  13,14,15,16,17,18]

如上，假设有3核，两个数组都等分成3个子数组，然后每个核合并一对子数组，最终得到一个合并完成的有序数组。一切看起来都没有问题。但是假设两个数组如下：

arr1 = [20,21,22,23,24,25,26,27,28]  split to --> [20,21,22]          [23,24,25]        [26,27,28]
arr2 = [10,11,12,13,14,15,16,17,18]  split to --> [10,11,12]          [13,14,15]        [16,17,18]
                                                  core0|              core1|            core2|
                                              [10,11,12,20,21,22,  13,14,15,23,24,25  16,17,18,26,27,28]

很不幸，上面的排序结果不对，因此，正确的数组划分成为了关键点。

论文提出了一种用于并行随机存取机 (Parallel Random Access Machines, PRAM) 的并行合并算法，即允许并发（并行）访问内存的共享内存架构。论文的算法具备负载均衡、无锁、高效内存访问的特点，仅需少量额外工作。为了实现高效的并行算法，论文提出了一种叫做 Merge Path 的方法，这也是论文的核心，下文将详细分析 Merge Path 的原理。

Merge Path

假设两个有序数组 \(A\) 和 \(B\)，长度分别为 \(|A|\) 和 \(|B|\)， \(A\) 和 \(B\) 构成矩阵 \(M\)，如下图所示：

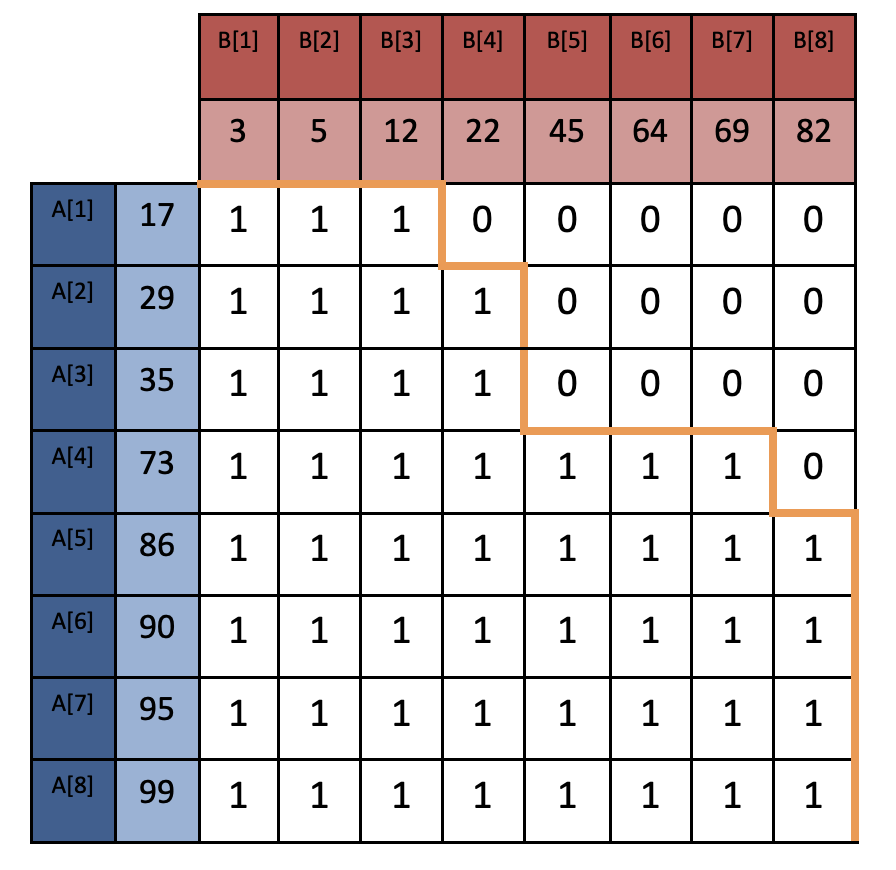
image-20230211205857408

声明：本文所有图片都来源于原论文。

我们来看下 Merge path 是如何构造的。要合并两个有序数组，我们从起点(1, 1)开始，比较 \(A[1]\) 和 \(B[1]\)，如果 \(A[1]>B[1]\)，将位置往右移动，否则往下移动，重复上述步骤直到走到右下方终点。最终得到一条路径（图中黄色路径），这条路径就称为 Merge Path。

通过构造 Merge Path 可以得出下面几个结论：

引理1：从头到尾遍历 Merge Path 的过程中，向右则选取 \(|B|\) 中未使用的最小值，向下则选取 \(|A|\) 中未使用的最小值，最终得到的结果即为合并后的有序数组。

引理2：合并路径上，任何连续片段都由 \(A\) 的连续元素序列和 \(B\) 的连续元素序列组成。

引理3：合并路径的非重叠片段由不相交的元素集组成，反之亦然。

引理4：对于合并路径上两个不相交的片段，后面片段的元素集肯定大于或等于前面片段的元素集。

定理5：考虑一组子数组对（来源于 \(A\) 和 \(B\))，这些子数组对包含了所有元素，它们一旦排序便形成了合并路径的连续片段。可以断言，这些子数组对可以并行合并，合并后的结果拼接在一起便形成了最终的有序数组。

推论6：将合并路径划分为任何个不重叠的片段，这些片段对应的子数组对都可以独立合并，合并后的结果按片段顺序串联形成一个合并路径上有序数组。

推论7：将合并路径平均划分为相同大小的片段，并行地合并片段对应的数组对，可以在多个处理器间达到负载均衡的效果。

并行合并和排序

有了上面的结论，我们来看下如何实现高效的并行合并算法。根据推论6和7，可以知道，需要将合并路径按照cpu核数平均划分，得到大小均匀的片段，然后并行地合并这些片段对应的数组对即可。要均匀地划分合并路径，其实就是要找到这些划分点，因此，算法的核心就是找这些划分点。算法核心思想如下：

  • 根据核数计算出每个线程处理的数据量
  • 对于每个线程，计算其所处理的起点偏移
  • 对于每个线程，根据起点偏移计算其在合并路径上对应的坐标点\((x, y)\)
  • 对于每个线程，根据自身的起点坐标点和终点坐标点(下一个线程的起点)合并数组对
  • 对于每个线程，将合并的结果写入最终数组对应的下标即可（根据前面的引理可知不同线程片段对应的元素集不会重复，因此这里不会出现内存并发安全问题）

通过上面的算法便能找到所有划分点，如下图：

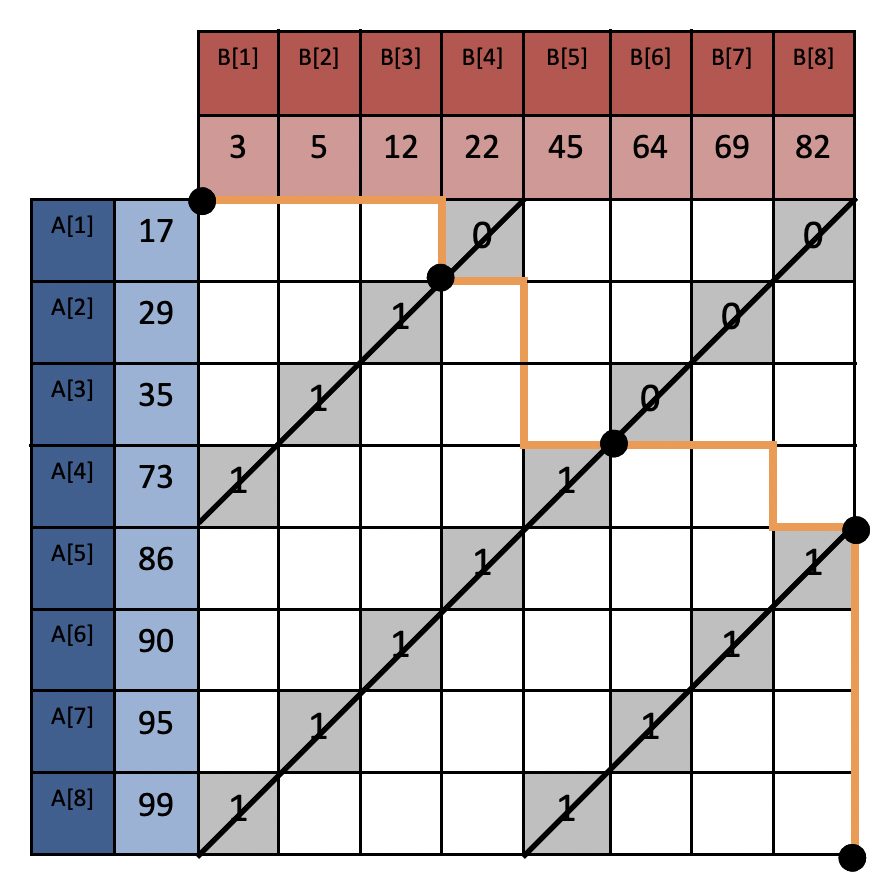
image-20230211230438935

划分点将合并路径平均分割，然后由每个线程独立地合并排序每个片段对应的数组对，得到最终的合并数组。论文提供了算法的实现代码，见 github地址 。笔者测了下，有点小bug（在某些情况下可能会coredump，笔者用Golang重新实现了算法，见 github地址 ）。

测试

测试环境：MacBook Air M1 芯片，逻辑核数 8

测试数据量：\(A\) 和 \(B\) 的size均为1亿，合并成2亿的数组

直接用论文提供的代码测试，测试结果如下：

$ make test100m
./a.out -A 100000000 -B 100000000 -t 2
OpenMP MergePath Implementation

Merging: A[100000000] B[100000000] to C[200000000] using 2 threads

serial merge 0.745051
Total OpenMP MergePath 0.379064
Speedup over serial merge 1.965501
MERGE SUCCESSFUL

Total Time 0.437201
./a.out -A 100000000 -B 100000000 -t 4
OpenMP MergePath Implementation

Merging: A[100000000] B[100000000] to C[200000000] using 4 threads

serial merge 0.745274
Total OpenMP MergePath 0.195741
Speedup over serial merge 3.807443
MERGE SUCCESSFUL

Total Time 0.231412
./a.out -A 100000000 -B 100000000 -t 8
OpenMP MergePath Implementation

Merging: A[100000000] B[100000000] to C[200000000] using 8 threads

serial merge 0.750698
Total OpenMP MergePath 0.132132
Speedup over serial merge 5.681429
MERGE SUCCESSFUL

Total Time 0.160297
./a.out -A 100000000 -B 100000000 -t 16
OpenMP MergePath Implementation

Merging: A[100000000] B[100000000] to C[200000000] using 16 threads

serial merge 0.750842
Total OpenMP MergePath 0.126917
Speedup over serial merge 5.916009
MERGE SUCCESSFUL

Total Time 0.164079

线程数从2到16递增，线程数越多，并发数越大，MergePath 算法也就越快。当然线程数并不是越多越好，最佳线程数和CPU配置有关系。从上面的结果可以看出，当线程数为16时，并行Merge比普通Merge快了将近6倍，说明并行Merge的实践表现效果非常优秀。

小结

本文主要解读了论文核心部分，还有些遗留内容并未解读，如果想了解更详细内容，可以直接看原论文。同时，笔者用Golang实现了论文中的算法（更加易懂），源码已上传github，感兴趣的同学可以阅读参考。

Reference