Main-Memory Hash Joins on Multi-Core CPUs/ Tuning to the Underlying Hardware 论文解读

Publish on: Classify at:
Words:3094 Read:≈ 7min Views: Comments:

这篇论文介绍了如何在多核 CPU 上结合底层硬件参数（能力）调优 Main-Memory Hash Joins 算法。

介绍

hash join 是一种常见的数据库操作，用于将两个表中的行通过一个共同的 join 键连接起来。hash join 通常可以分为基于磁盘和基于内存两种方式。在基于磁盘的 hash join 中，数据需要从磁盘读入内存，这样可能会导致高延迟和低效率。相比之下，基于内存的 hash join 通常比较快速和高效。

然而，随着多核 CPU 的出现，基于内存的 hash join 也面临着一些新的挑战。在多核 CPU 上，数据的并发读写可能会导致缓存争用和内存带宽瓶颈等问题，从而影响 hash join 的性能。因此，需要对基于内存的 hash join 算法进行优化，以充分利用多核 CPU 的计算能力和内存带宽。该论文旨在提出一种针对多核 CPU 的主存 hash join 方法，并优化该方法以适应底层硬件的特性。

BACKGROUND: IN-MEMORY HASH JOINS

现有的算法可分为两大阵营，一种是 *Hardware-oblivious（硬件无感）*的 hash join，即算法不考虑硬件相关的参数，相反，他们从现代硬件的特征考虑，认为可以在任何技术相似的硬件上取得良好的性能，代表有 no partitioning join。

另一种是 *Hardware-conscious（硬件有感）*的实现，这种方法旨在通过调整算法参数（如 hash table 大小等）来最大化利用硬件特性，代表有 radix join。

Canonical Hash Join Algorithm

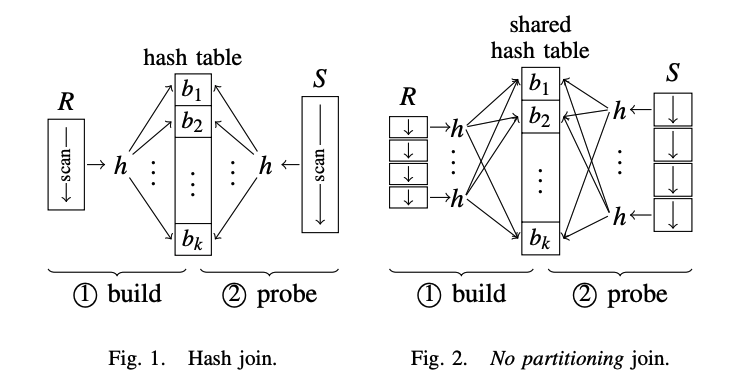
image-20230320234439659

任何现代 hash join 实现的基础都是 canonical hash join，canonical Hash Join 算法的主要思想是将两个表的连接操作转化为一个哈希表的建立和查找操作。主要分为两个阶段：build phase 和 probe phase。算法如上图 Fig. 1 所示，步骤如下：

  1. Scan 较小表 \(R\)，并对其中的 join 列建立哈希表，哈希表的键为 join 列的值，哈希表的值为连接列所在行的指针或行的副本
  2. Scan 较大表 \(S\)，对于每一行，使用哈希函数计算连接列的哈希值，查找哈希表中对应的条目，并与当前行进行匹配
  3. 如果匹配成功，则将两个表的对应行合并，并输出到结果集中
  4. 如果没有匹配，则继续处理下一行
  5. 处理完所有行之后，输出结果集

两个表都需要 scan 一次，假设 hash 表的访问是常数时间开销，那么 canonical hash join 算法的时间复杂度为 \(O(|R|+|S|)\)。

No Partitioning Join

为了利用现在并行硬件的优势，业界提出了一种 canonical hash join 算法的变体 no partitioning join。该算法中的 no partitioning 指的是不对哈希表分区，但是会对数据表分区。这种算法不依赖硬件的任何特定参数，该算法如上图 Fig. 2 所示。

两张表都会被均分成多个部分（portions），这些 portions 会分配给多个线程并行处理。在 build phase，所有线程都会 scan 自己负责的 portions 生成一个全局的哈希表。由于哈希表是所有线程共享的，也就意味着向哈希表插入数据需要 synchronized，线程在向哈希表中的 bucket 插入数据时，需要先上锁，上锁成功后才能插入数据。论文指出这里潜在的锁竞争会比较少，因为哈希 bucket 的个数往往比较多，由于锁是 bucket 粒度的，所以锁冲突的概率比较低。

probe phase 访问哈希表是只读模式，因此在该阶段不用加锁，并行访问的效率会很高。假设系统有 \(p\) 个核，那么该算法在理想情况下（build phase 锁冲突概率极低）的时间复杂度为 \(O(1/p(|R|+|S|))\)。

Radix Join

哈希表可以通过 key 的哈希值直接访问，效率很高，但是随机访问内存也会带来 cache misses 问题。论文中引用了其他论文说明了 cache misses 会影响查询性能。业界也证明了当哈希表的大小大于了 cache 大小，几乎每次哈希表的访问都会导致 cache miss。因此，将哈希表划分成 cache 大小的块可以减少 cache misses，从而提高性能。同时，论文还提到在分区阶段，需要考虑 TLB misses 的问题，这样便引出了 radix join 算法。

Partitioned Hash Join

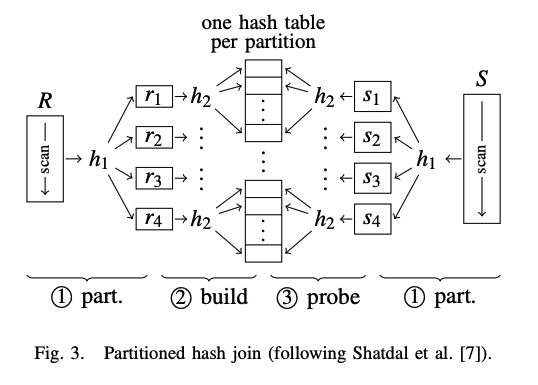
image-20230321223511075

如上图 Fig. 3. 第一阶段，关系表 \(R\) 和 \(S\) 经过哈希函数 \(h1\) 哈希分区为 \(ri\) 和 \(sj\)；在 build phase，针对每个分区 \(ri\) 通过哈希函数 \(h2\) 构建单独的哈希表，由于每个分区对应一个哈希表，这样哈希表的大小便能适配 CPU cache；在 probe phase，scan \(sj\) 并在对应的哈希表中查找匹配的 tuples 做 join。

由于在 partitioning phase，\(R\) 和 \(S\) 使用相同的哈希函数 \(h1\) 做哈希分区，因此可以得出以下结论： $$ ri \Join sj = \emptyset (i\neq j) $$ 通过哈希分区构建哈希表的方式，解决了哈希表过大导致 cache misses 的问题，但同时又引来了新的问题。由于 \(h1\) 的散出可能很大，哈希分区会产生特别多的 partitions，这些 partitions 往往分布在不同的内存页里。我们知道，操作系统里面内存管理的方式是将内存划分为页来管理，进程通过虚拟地址来访问内存时，需要访问页表找到对应的物理页进而找到对应的物理地址，从而实现地址转换。

地址转换的开销是比较大的，操作系统需要通过 TLB 这一高速缓存来缓存经常被用到的页表项，从而提升地址转换的速度。由于 partitions 可能会比较多，从而会占用很多内存页，进而导致内存页数远远超过 TLB 所能缓存的页表项，那么在访问 partitions 时大概率会导致 TLB misses，造成性能问题。

Radix Partitioning

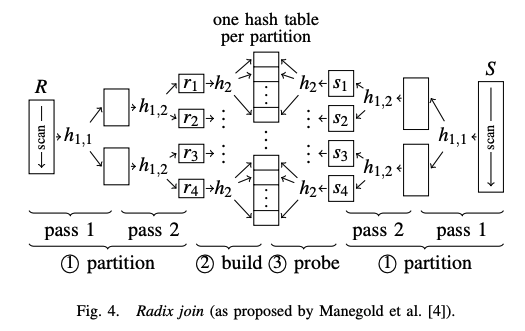
image-20230322225729922

通过简单的哈希分区，会导致 TLB misses 问题，为了解决这一问题，引出了一种新的分区方法 radix partitioning，如上图 Fig. 4. radix partitioning 会分成多轮（pass），每一轮选取 join 键的不同 bits 来哈希分区，下一轮的输出作为下一轮的输入，通过多轮的方式保证最终的散出不超过 TLB 最大缓存页表项数。由于每一轮都是选取的不同位（a different set of bits），类似基数排序每轮选取不同位排序，因此这种分区算法叫做 radix partitioning。

介绍完 radix partitioning，再来讲 radix join 就比较好理解了，步骤和上述类似：

  1. 通过 radix partioning，将 \(R\) 和 \(S\) 划分为数量可控的 \(ri\) 和 \(sj\)
  2. 对每个 \(ri\) 构建单独的哈希表
  3. scan \(sj\) 在对应的哈希表中查找匹配的 tuples 做 join

在 radix partitioning 的多轮分区中，每轮最大散出时根据硬件参数来固定设置的，那么 paritioning 的轮数为 \(log|R|\)，因此 radix join 的时间复杂度为 \(O((|R|+|S|)log|R|)\)。

radix join 需根据硬件调整的参数如下：

  1. 每轮 radix partitioning 的最大散出需要根据硬件支持的 TLB 数来限制
  2. 生成的分区大小需要大致（不能大于）和 CPU cache 保持一致

Parallel Radix Join

radix join 能够并行化处理，需要将关系表切分成多个子表，将这些子表分配给多个线程，每个线程将自己负责的子表哈希到相应的 partitions，根据上一节讲的，需要考虑硬件参数来限制数量，因此 partitions 的数量不会太多。由于多个线程都会往 partitions 写数据，因此这里存在潜在的竞争问题，由于 partitions 的数量有限，这里竞争的概率就比较大（对比 no partitioning join 低概率竞争）。

为了避免线程竞争问题，这里有个比较有意思的做法是，每个 partiton 预先为每个线程保留相应大小区间范围，然后每个线程计算写入 partiton 的位置，将对应的数据写入相应位置即可。这里由于每个线程写入的位置一定不同，所以可以不用加锁同步。论文其实没有详细讲并行 partitioning 的具体方法，为了便于理解，下面引用 CMU Andy Pavlo 教授的课件来讲解下并行 radix partitioning 的步骤。

第一步，每个线程 scan 子表，然后统计 radix hash 后各个 partiton 的 histogram（其实就是每个 partition 的 tuple 个数），如下图：

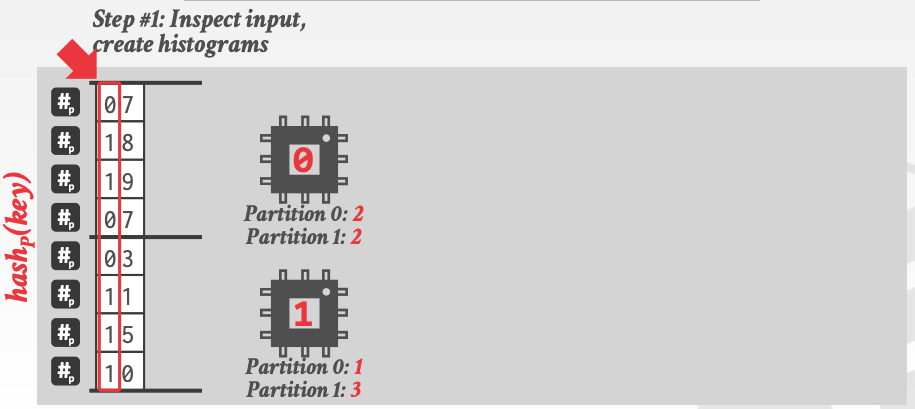
image-20230323231418607

第二步，计算每个线程输出的偏移位置，第一步完了后，其实可以得到一个序列如下：

2 1 2 3 // 分别表示 thread-0 在 partition-0, thread-1 在 partiton-0, thread-0 在 partiton-1，thread-1在 partition-1 中的数量

然后根据上述序列可以生成一个序列，叫做 prefixSum 如下：

0 0+2 0+2+1 0+2+1+2 => 0 2 3 5 // 每个值代表上述序列每个元素位置的前缀和

计算出的 prefixSum 序列就是各线程在 partitons 中的偏移位置，如下：

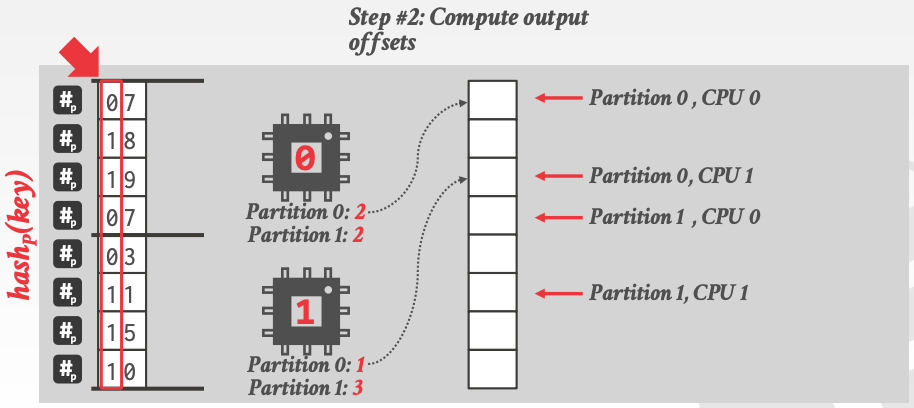
image-20230323233052998

第三步，每个线程再一次 scan 子表，将数据写入 partitions 相应位置，如下：

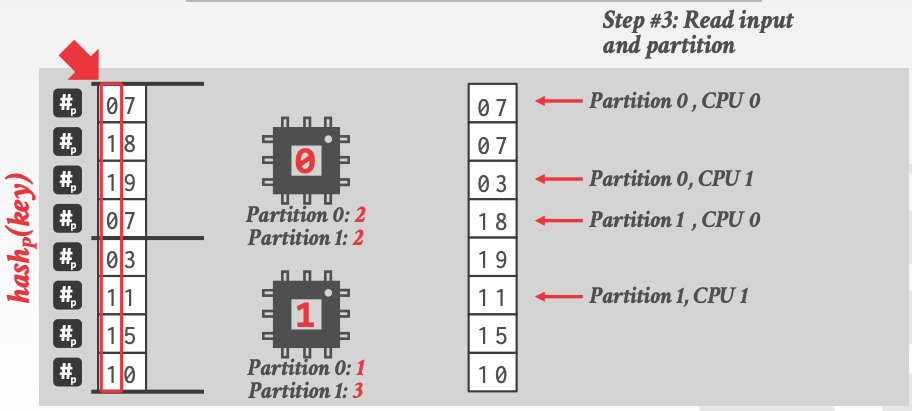
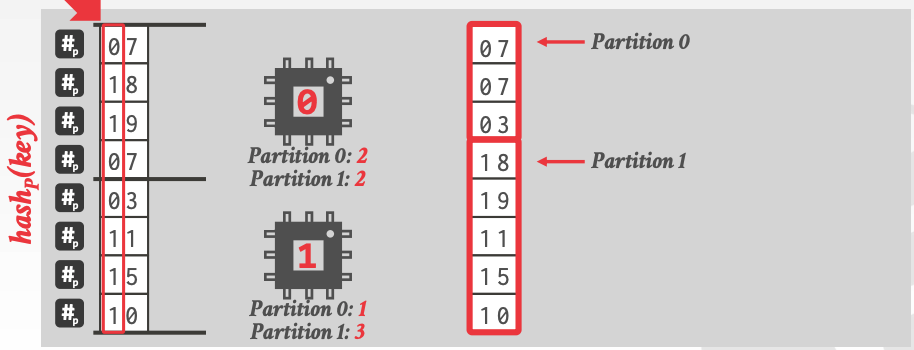
image-20230323233226996 image-20230323233437201

最后，选取其他 bit，递归上述的 parallel radix partitioning 步骤，直到得到目标个数的 partitions：

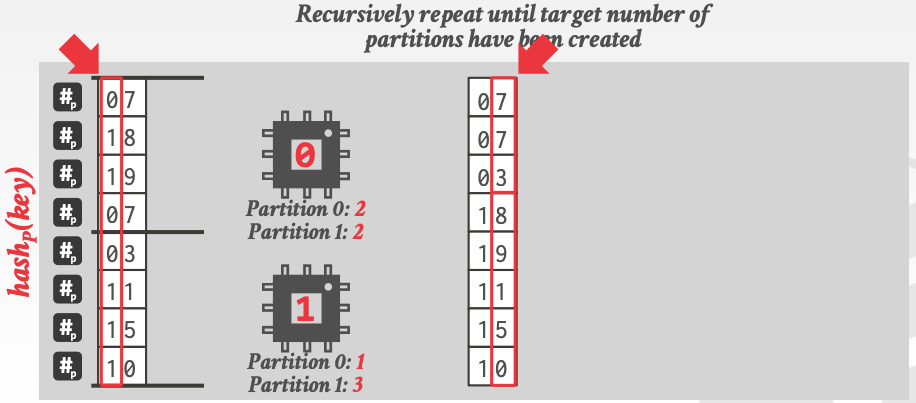
image-20230323233706205

通过上面的讲解，并行 radix partitioning 的实现原理应该比较清晰了。partitioning 完毕后，后面的 build 和 probe 不存在线程竞争，可以抽象成 task，交给线程池并行处理。到此，整篇论文的原理讲解完毕。

小结

本文主要解读了论文的核心原理，论文实验数据部分没有贴上来，大家感兴趣可以查看原始论文。本文整体讲解脉络和论文保持一致，有些地方是笔者根据自己的理解来叙述讲解的，如果不当之处，欢迎指正！

Reference