Fastest table sort in the West - Redesigning DuckDB’s sort
本文是阅读 DuckDB 技术博客 《Fastest table sort in the West - Redesigning DuckDB’s sort》 后的翻译,同时插入了个人的理解和总结。
提到排序,可能很多同学会觉得这种常规操作 so easy,各种排序算法都比较成熟,很多语言的标准库都提供了排序算法的实现,研究的意义不是很大。但是在数据库系统中,排序不是简单针对一批数值或者字符串,而是整个数据表。排序涉及复杂的比较和数据移动,而且对于内存和外存考虑点也不尽相同,要实现一个高效灵活的排序算法不是一件容易的事情。
DuckDB 在排序上做了很多优化,性能也非常亮眼,我们来看看 DuckDB 究竟在排序上做了哪些优化。
排序关系数据
排序是计算机科学中充分研究的问题之一,它是数据管理的一个重要方面。对排序算法的研究往往聚焦于对大型数组或键值对。但是这并没有覆盖到在数据库系统中怎么实现排序。对数据表排序远不止对大量整数数组排序那么简单!
考虑以下对 TPC-DS 表片段的示例查询:
SELECT c_customer_sk, c_birth_country, c_birth_year
FROM customer
ORDER BY c_birth_country DESC, c_birth_year ASC NULLS LAST;
结果:
| c_customer_sk | c_birth_country | c_birth_year |
|---|---|---|
| 64760 | NETHERLANDS | 1991 |
| 75011 | NETHERLANDS | 1992 |
| 89949 | NETHERLANDS | 1992 |
| 90766 | NETHERLANDS | NULL |
| 42927 | GERMANY | 1924 |
数据首先按照 c_birth_country 降序排序,在 c_birth_country 相同的情况下按 c_birth_year 升序排序,NULL 值被当做最大值处理。整行数据被重新排序后,不仅仅是参与排序的字段列被重排,其他未在 ORDER BY 中的列(称为 “payload columns”)也会被重排,如上述例子中的 c_customer_sk。
可以很容易地使用任何排序算法,如 C++ 中的 std::sort 对数据排序,尽管 std::sort 是一个十分出色的算法,但它仍然是一种单线程方法,无法有效地按多列进行排序,因为函数调用开销会很快占据排序时间。下面我们将讨论为什么会这样。
排序的成本主要是比较值和移动数据。能够让这两个操作代价更低的任何事情都会对总运行时间产生重大影响。
当我们有多个 ORDER BY 子句时,有两种明显的方法可以实现比较器:
- 遍历子句:比较列,直到我们找到一个不相等的列,或者直到我们比较了所有列。这已经相当复杂了,因为对行数据进行比较时,需要循环比较所有列(函数调用开销大),判断大小(一个循环内部需要包含一个 if/else,分支预测降低 cpu 执行效率),如果是列存存储,那么在比较不同列时,会造成内存的随机访问(读完一行中的 a 列,然后读 b 列,… ,不同列在物理上不连续,容易导致 cache missing)
- 按第一个子句完全排序数据,然后按第二个子句排序,但仅对第一个子句相等的数据排序,依此类推。当有很多重复值时,这种方法效率特别低,因为它需要多次遍历数据。
针对上述两种方法,这里举个简单例子解释下更容易明白。假设有数据表 t1 如下:
| id | city | name |
|---|---|---|
| 1 | BeiJing | Zhang |
| 2 | ChengDu | Xie |
| 3 | BeiJing | Wang |
| 4 | HangZhou | Liu |
| 5 | GuangZhou | Li |
查询语句为:
SELECT id, city, name
FROM t1
ORDER BY city DESC, name ASC;
使用方法 1 比较时,和传统的排序比较一样,两行数据比较时同时比较 city 和 name,如果 city 不同则比较结束,否则再比较 name。这样只需一轮排序便可以得到最终排序结果。算法如下图:
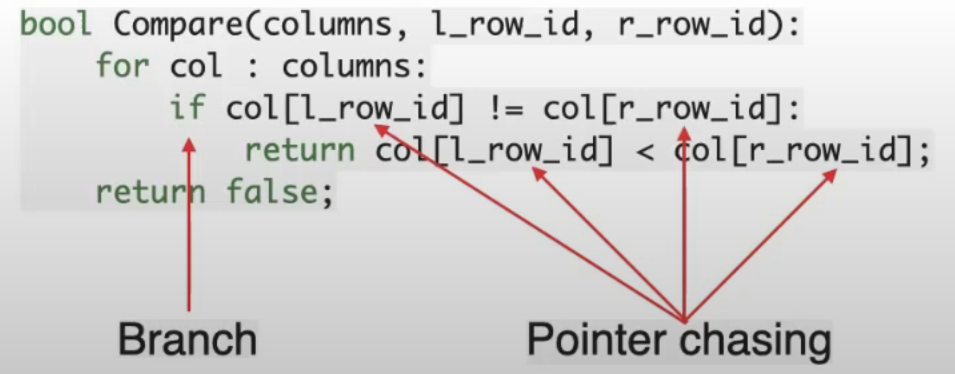
注意图中两个关键词 Branch 和 Pointer chasing,正好对应这种比较算法的缺点:
- 分支预测,降低 CPU 执行效率
- 内存随机访问效率低(相对顺序访问)
使用方法 2 比较时,第一轮,先按 city 比较排序,结果如下:
| id | city | name |
|---|---|---|
| 1 | BeiJing | Zhang |
| 3 | BeiJing | Wang |
| 2 | ChengDu | Xie |
| 5 | GuangZhou | Li |
| 4 | HangZhou | Liu |
由于 city 有重复,只比较 city 不能得到最终排序结果,还需第二轮按照 name 比较排序,结果如下:
| id | city | name |
|---|---|---|
| 3 | BeiJing | Wang |
| 1 | BeiJing | Zhang |
| 2 | ChengDu | Xie |
| 5 | GuangZhou | Li |
| 4 | HangZhou | Liu |
可以看到,方法 2 每轮比较的字段一样,在数据重复较多时,会导致多轮排序。
二进制字符串比较
二进制字符串比较技术通过简化比较器来提高排序性能。将 ORDER BY 子句中的所有列编码为单个二进制序列,当使用 memcmp 进行比较时将产生正确的排序顺序。对数据编码是有代价的,但由于在排序过程中大量使用比较器,因此付出这种代价是有价值的。让我们再看一下示例的 3 行:
| c_birth_country | c_birth_year |
|---|---|
| NETHERLANDS | 1991 |
| NETHERLANDS | 1992 |
| GERMANY | 1924 |
在little-endian硬件上,表示这些值的字节在内存中看起来像这样,假设 c_birth_year 为 32 位整数表示:
c_birth_country
-- NETHERLANDS
01001110 01000101 01010100 01001000 01000101 01010010 01001100 01000001 01001110 01000100 01010011 00000000
-- GERMANY
01000111 01000101 01010010 01001101 01000001 01001110 01011001 00000000
c_birth_year
-- 1991
11000111 00000111 00000000 00000000
-- 1992
11001000 00000111 00000000 00000000
-- 1924
10000100 00000111 00000000 00000000
那怎么将这些二进制编码为字符串才能满足需求呢?做法如下:
- 固定二进制字符串大小,便于在排序过程中移动。不足大小的字符串以 00000000 填充,反之,如果字符串太大,只需要编码其前缀,只有当前缀相同时再比较整个字符串
- 降序字段的二进制取反(0变1,1变0),如示例中的 c_birth_country
- 升序排序字段的二进制按大端(高字节在地址,低字节在高地址,符合字符串处理顺序)编码表示,同时符号位(第一位)取反(1变0,0变1,保证负数的二进制字符串小于非负数)
按上面的编码方式得到二进制字符串如下:
-- NETHERLANDS | 1991
10110001 10111010 10101011 10110111 10111010 10101101 10110011 10111110 10110001 10111011 10101100 11111111
10000000 00000000 00000111 11000111
-- NETHERLANDS | 1992
10110001 10111010 10101011 10110111 10111010 10101101 10110011 10111110 10110001 10111011 10101100 11111111
10000000 00000000 00000111 11001000
-- GERMANY | 1924
10111000 10111010 10101101 10110010 10111110 10110001 10100110 11111111 11111111 11111111 11111111 11111111
10000000 00000000 00000111 10000100
根据上面的规则生成二进制字符串后,现在可以通过只比较二进制字符串来同时比较两列。在 C++ 中使用单个 memcmp 函数即可完成比较,编译器将为单个函数调用生成高效的汇编,甚至自动生成 SIMD 指令(Why?)。
该技术解决了复杂比较带来的函数调用开销。
基数排序
现在我们有了一个高效的比较器,我们得选择一个排序算法。计算机科学的同学都学习过基于比较的排序算法,例如 Quicksort 和 Merge sort,它们的时间复杂度为 \(O(nlogn)\),其中 \(n\) 是要排序的记录数。
然而,也有基于分布的排序算法,它们的时间复杂度通常为 \(O(nk)\) 其中 \(k\) 是排序键的宽度。由于 \(k\) 是常数,而 \(logn\) 不是,因此这类排序算法在 \(n\) 越大的情况下越有优势。基于分布排序之一的算法是基数排序,该算法通过使用计数的方法计算数据分布从而实现对数据的排序,多次执行这种方法直到所有位都计算完毕。
对排序键列进行编码,这样我们就有了一个高效的比较器,然后选择一个基于分布而不是比较的排序算法,这听起来可能矛盾。然而,编码对于基数排序是必要的:使用 memcmp 比较二进制字符串将产生正确的顺序,那么如果我们逐字节进行基数排序也能产生正确的顺序。
个人理解,如果使用基数排序,那么二进制字符串编码的主要目的是保证编码能够不改变原始比较的结果,且编码长度是固定位,也正好适用于基数排序。
两阶段并行排序
DuckDB 使用 Morsel-Driven Parallelism ,这是一个用于并行查询执行的框架。对于排序操作,这意味着多个线程从表中并行收集大致相等数量的数据。
推荐阅读论文 Morsel-Driven Parallelism 解读文章 https://zhuanlan.zhihu.com/p/378534053
我们使用这种并行性进行排序,首先让每个线程使用基数排序对它收集的数据进行排序。在第一个排序阶段之后,每个线程都有一个或多个已排序的数据块,这些数据块必须合并得到最终的排序结果。归并排序是此任务的首选算法,归并排序的实现方式主要有两种: K-way merge and Cascade merge .
K-way merge 将 K 个列表一次合并为一个排序列表,并且常用于外部排序(对超过内存的数据进行排序),因为它最大限度地减少了 I/O。Cascade merge 一次合并两个已排序数据列表,直到只剩下一个已排序列表,用于内存排序,因为它比 K-way merge 更高效(思考这是为什么)。我们的目标是拥有一个具有高内存性能的实现,当我们超过可用内存的限制时,它会优雅地降级(这里降级指的什么?换成其他 Merge 算法?)。因此,我们选择 Cascade merge。
在 Cascade merge sort 中,我们一次合并两个已排序数据块,直到只剩下一个已排序数据块。自然地,我们希望使用所有可用的线程来计算合并。如果我们有比线程更多的排序块,我们可以让每个线程来合并块(每个线程都有活干)。然而,随着块的合并,我们将没有足够的块来保持所有线程忙碌(活少了,有些线程便会空闲)。当合并最后两个块时,这特别慢:一个线程必须处理所有数据。
为了完全并行化这一阶段,我们采用了 Oded Green 等人的 Merge Path 。Merge Path 会预先计算排序列表在合并时相交的位置,可以使用二分搜索有效地计算沿合并路径的交叉点。如果我们知道交叉点在哪里,我们就可以并行地独立合并排序数据的分区。这使我们能够在整个合并阶段有效地使用所有可用线程。
Merge Path 这个技术点请阅读文章 https://zhuanlan.zhihu.com/p/606678298
列还是行?
除了比较之外,排序的另一大成本是移动数据。 DuckDB 有一个向量化的执行引擎。数据以列式布局存储,一次分批(称为 Chunks 块)处理。这种布局非常适合分析查询处理,因为块适合 CPU 缓存,并且它为编译器提供了很多生成 SIMD 指令的机会(列数据聚簇,可以同时处理)。然而当表被排序后,整行都会重新打乱排序,而不仅仅是参与排序的列。
我们可以在排序时坚持按列布局:对关键列进行排序,然后对 payload columns 一个一个重排序。但是,对每列重新排序将导致内存的随机访问。如果 payload 列很多,这会很慢。将列转换为行将使重新排序行变得更加容易。这种转换当然不是没有代价的:需要将列复制到行,并在排序后再次从行复制回列(数据本身是按列存储的,在排序的时候将列存转化为内存中的行存,排完后再转为列)。
因为我们想要支持外部排序,所以我们必须将数据存储在可以卸载到磁盘的缓冲区管理块中。因为无论如何我们都必须将输入数据复制到这些块中,所以将行转换为列实际上是没有额外代价的。
有一些运算符本质上是基于行的,例如连接和聚合。 DuckDB 对这些运算符有一个统一的内部行布局,我们决定也将它用于排序运算符。到目前为止,这种布局只在内存中使用过。在下一节中,将解释我们是如何让它在磁盘上工作的。应该注意,如果主内存无法容纳,我们只会将排序数据写入磁盘。
外部排序
缓冲区管理器可以将块从内存卸载到磁盘。我们在排序实现中不会主动将内存块写入磁盘,而是由缓冲区管理器在内存填满时来触发。它使用 LRU 队列来决定哪些块将写入磁盘。
当需要一个块时,我们固定(pin)它,如果需要的块不在内存中,将会从磁盘读取它。访问磁盘比访问内存慢得多,因此尽量减少读写次数是至关重要的。
将数据卸载到磁盘对于固定大小的列(如整数)很容易,但对于可变大小的列(如字符串)则更难(Why)。我们的行布局使用固定大小的行,不能容纳任意大小的字符串。因此,字符串由一个指针表示,该指针指向实际字符串数据所在的特定内存块,即所谓的 “string heap”。
我们已经更改了堆,以便在缓冲区管理的块中也逐行存储字符串:
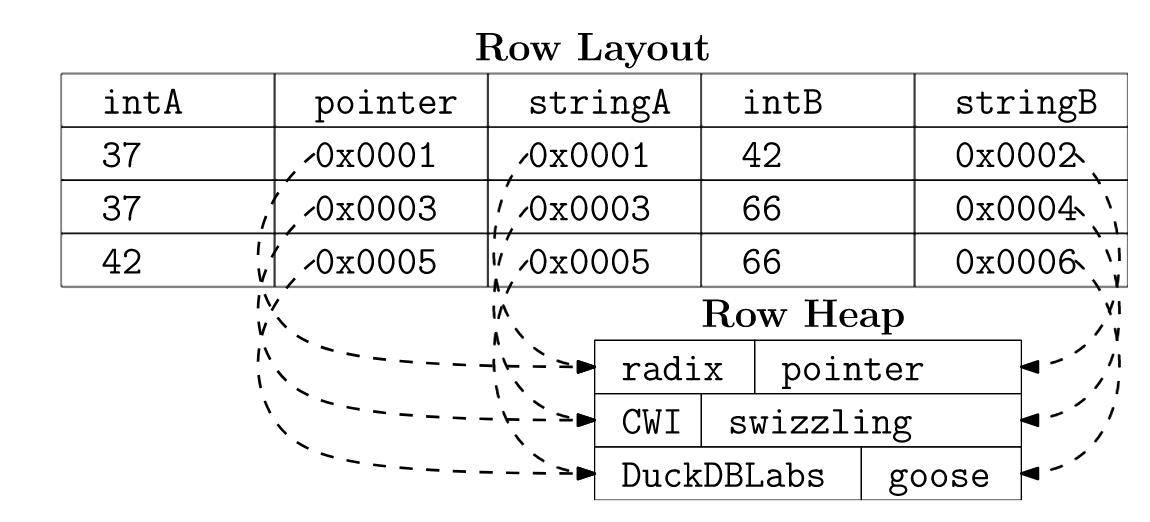
每行都有一个额外的 8 字节字段指针,指向堆中该行的开头。这在内存表示中是无用的,但稍后我们将看到为什么它对磁盘表示有用。如果内存能放下数据,堆块将保持固定状态,并且在排序时仅对固定大小的行进行重新排序。如果内存放不下数据,则需要将块卸载到磁盘,并且堆在排序时也会重新排序。当堆块卸载到磁盘时,指向它的指针将失效。当我们将块加载回内存时,指针将会改变。
这就是我们的行式布局发挥作用的地方。 8 字节的指针字段被 8 字节的偏移量字段覆盖,表示在堆块中可以找到该行字符串的位置。这种技术称为 “pointer swizzling” 。当我们调整指针时,行布局和堆块看起来像这样:

指向后续字符串值的指针也被一个 8 字节的相对偏移量覆盖,表示该字符串距堆中行开头的偏移量(因此每个 stringA 的偏移量为 0:它是行中的第一个字符串)。在排序期间使用行内的相对偏移量而不是绝对偏移量非常有用,因为这些相对偏移量保持不变,并且在复制行时不需要更新。当需要扫描块以读取排序结果时,我们“unswizzle”指针,使它们再次指向字符串。
通过这种双重用途的按行表示,我们可以轻松地复制堆中固定大小的行和可变大小的行。除了让缓冲区管理器加载/卸载块之外,内存中排序和外部排序之间的唯一区别是我们 swizzle/unswizzle 指向堆块的指针,并在归并排序期间从堆块复制数据。
上述技术减少了由于内存不够带来的性能开销。
Comparison with Other Systems
排序算法经过精心设计后,当然要和其他数据库管理系统比较才能证明 DuckDB 的性能优势,选取比较的系统如下:
- ClickHouse , version 21.7.5
- HyPer , version 2021.2.1.12564
- Pandas , version 1.3.2
- SQLite , version 3.36.0
比较结果就不贴了,可以直接看原文。
结论
DuckDB 新的并行排序实现可以有效地对超出内存容量的数据进行排序,从而利用现代 SSD 的速度。在其他系统因为内存不足而崩溃或者切换到速度慢得多的外部排序算法的情况下,DuckDB 的性能在超过内存限制时优雅地下降(也就是说内存不足时,DuckDB 的性能下降得不是那么陡)。
总结
本文翻译+总结了文章 《Fastest table sort in the West - Redesigning DuckDB’s sort》。这篇文章涉及的技术远不止排序,涉及了计算机中很多重要的基础知识,技术点比较细腻,需要扣细节并深入思考才能更好地理解。