高效内存索引:Adaptive Radix Tree
自适应基数树(Adaptive Radix Tree)是一种高效的数据结构,用于存储和检索键值对。它是一种自适应的树结构,根据实际数据的分布情况来调整内部节点的结构,以提高性能和减少存储空间的使用。
Trie
Trie(也称为字典树或前缀树)是一种特殊的树型数据结构,用于有效地存储和检索字符串集合。Trie 的主要特点是将字符串分解成单个字符,并将每个字符存储在一个节点上。从根节点开始,每个节点都代表一个字符,通过连接各个节点来表示完整的字符串。Trie 的根节点通常不存储实际字符,而是用于连接所有的子节点。如下图:
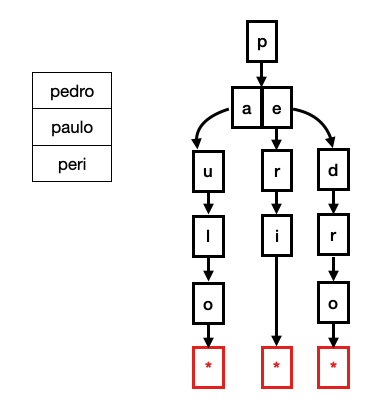
在 trie 中查找某个 key,需要从根节点开始,根据要查找的字符串逐级向下遍历。如果在任何层级上找不到对应的子节点,则表示字符串不存在于 Trie 中。
比如,要查找字符串 pedro, 那么需要先查找根节点是否包含字符 p,如果包含,那么检查下一层是否包含字符 e,如此这般,直到最后一个字符也包含在一个终止节点(表示从根节点到该节点为一个完整字符串),如下图蓝色路径则为字符串 pedro 的查找路径。
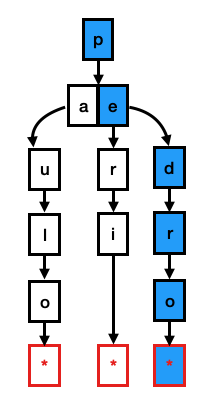
Trie 的主要优点是:
- 高效地插入和查找字符串,时间复杂度为 $O(k)$,其中 $k$ 是字符串的长度。
- 可以高效地进行前缀匹配,用于实现自动补全、单词搜索等。
实际上,Trie 也可以用来存储数值类型的数据。对于 uint64 的数值,最大为 18,446,744,073,709,551,615。如果按字符来存储,那么存储 uint64 的最大值需要 17 层,显然这种存储方式并不高效,那么如果我们按 bits 存储呢?uint64 有 64-bits,每个节点的 key 用 8-bits 表示,那么只需要 8 层即可。
我们以每个节点存 2-bits 为例,假设 Trie 中存储了 7, 10, 12,从下图可以看到这三个数的二进制表示。每个节点的值由 0 和 1 组成,同时每个节点包含指向所有子节点的指针,指针为 * 代表该子节点存在,指针为 Ø 代表改子节点不存在。最终由叶子节点指向实际的数据。
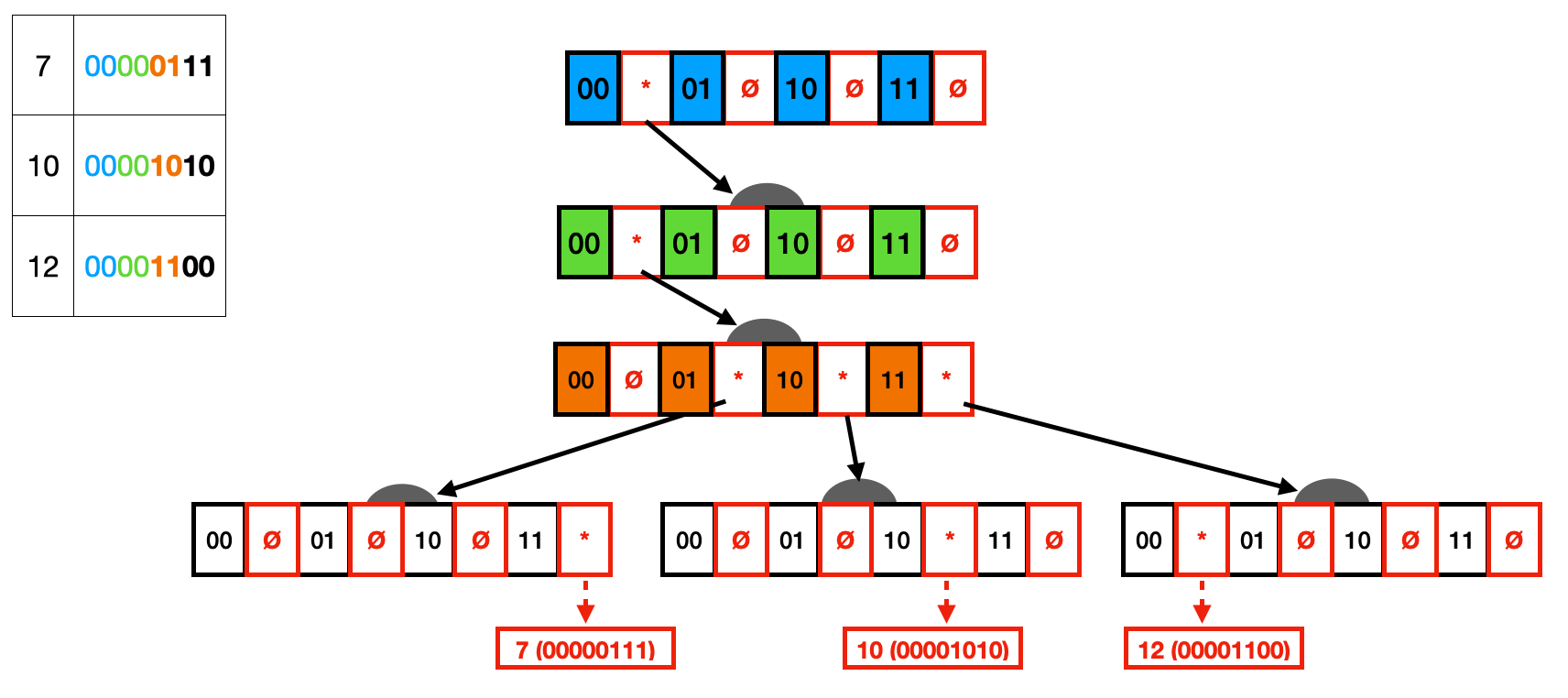
然而,我们可以很容易看出,上述 Trie 有两个缺点:
- 有的节点只有一个子节点,既增加了层级也浪费了空间
- 有的节点存在大量空指针,浪费空间。
为了解决上述问题,一般使用压缩技术来达到节约空间的目的。
Radix tree
Radix tree(基数树,也称为压缩前缀树或 Patricia 树)是一种特殊的多叉树数据结构,用于高效地存储、检索和查找字符串键(key)和与之相关联的值(value)。它被广泛用于实现诸如IP路由表、字典、自动补全和编译器等应用。
Radix tree 的思想是通过在垂直方向折叠只含有一个子节点的节点来达到压缩的效果,这个过程在论文里称为路径压缩(Path Compression)。如下:
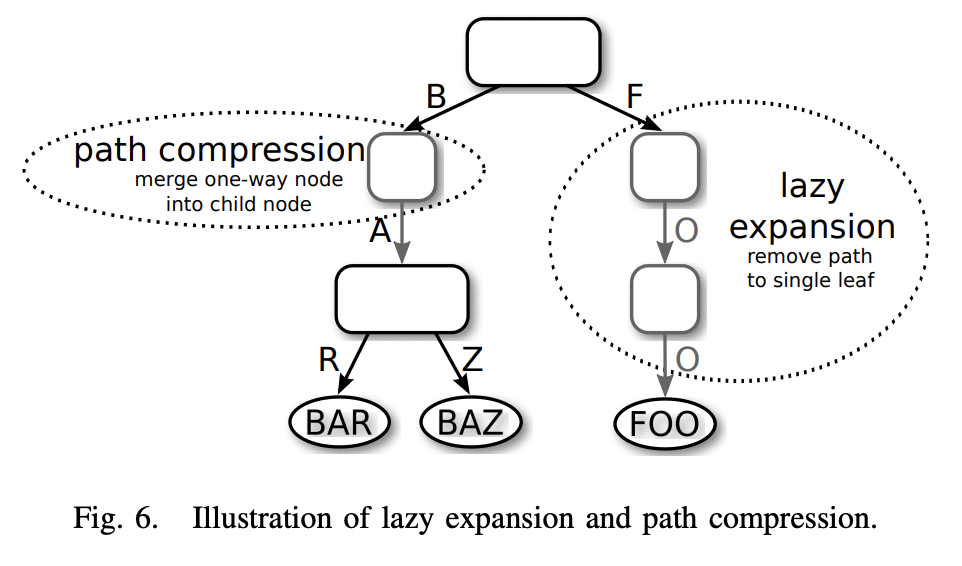
压缩后的节点需要将路径的前缀存储下来,如下:
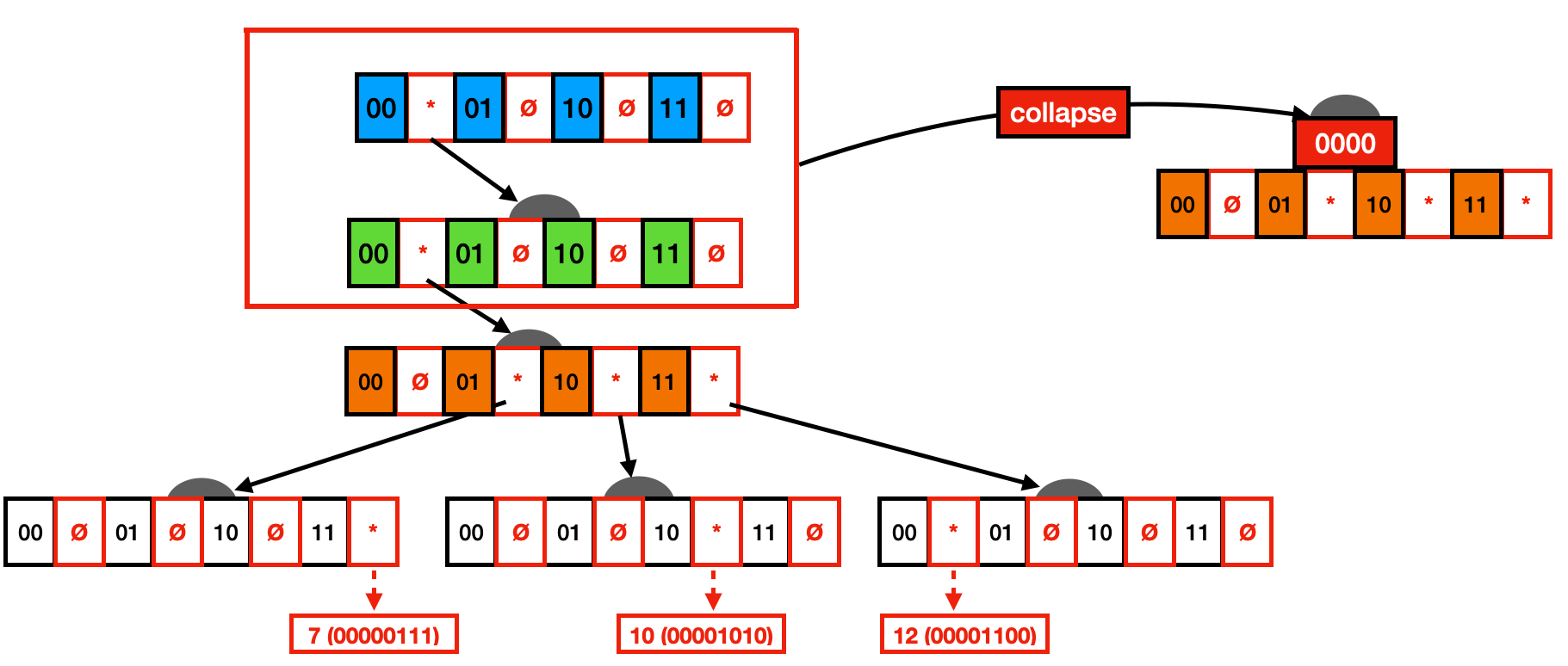
前两层的节点都只有一个子节点,将它们折叠到第三层的节点,保存折叠路径的前缀 0000,形成一个新节点,如下所示:
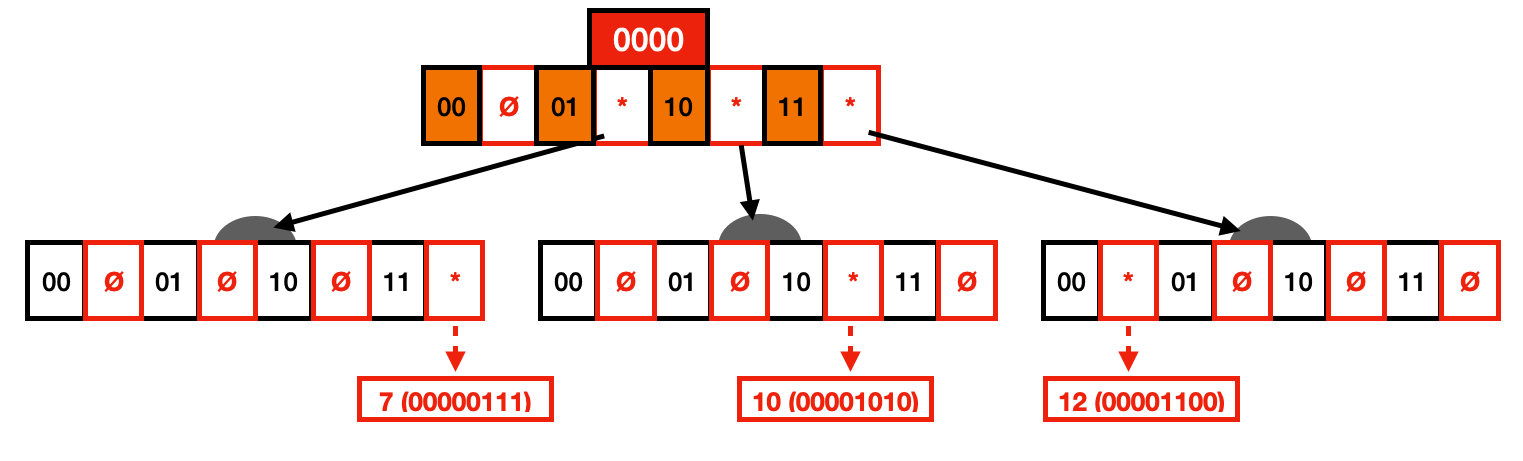
查找时,遇到折叠过的节点,要比较前缀是否匹配。经过垂直压缩,减少了节点树和层级树,节约了大量空间,但是依然没有解决空指针浪费的问题。
Adaptive Radix Tree
ART (自适应基数树) 的关键就在于 Adaptive 这个词,为了充分理解 ART 的设计精髓,我们还是以一个例子入手。我们以一个节点存 8-bits 为例,如下:
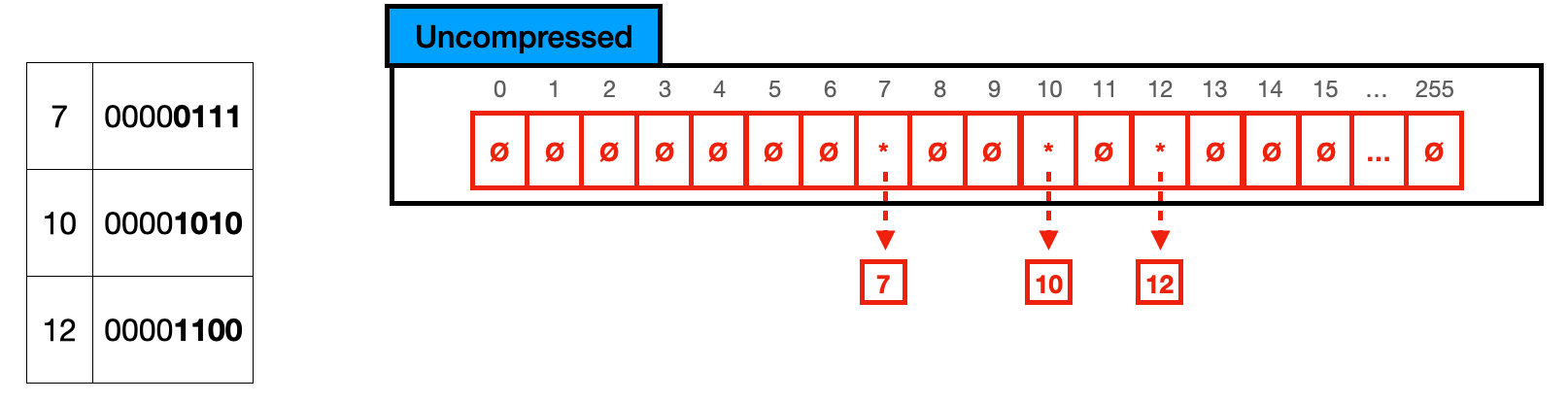
可以看到,节点将存 256($2^8$)个指针,指针数组的下标代表子节点的值。整个节点占用的空间为 2048(256 * 8)bytes,然而实际有效的指针只有 3 个,也就意味着有 2024 (2048 - 24)bytes 浪费掉了。
为了解决上述空指针浪费的问题,ART 便应运而生。ART 的思路是提供 4 种不同类型的节点,并根据当前节点有效指针数量选取合适的节点类型。4 种节点类型如下:
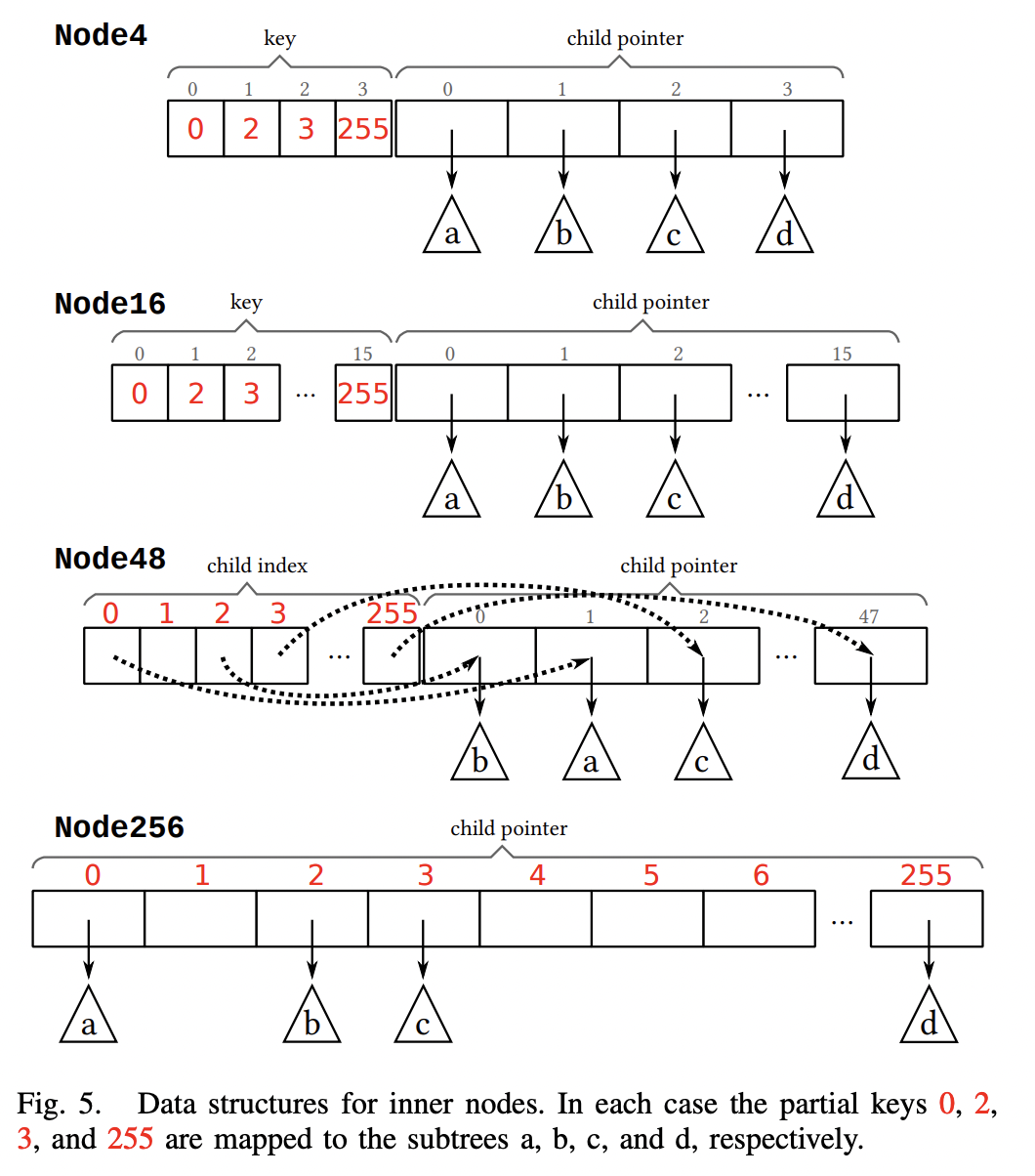
Node4,由一个长度为 4 的 byte 数组和长度为 4 的指针数组构成,最多存储 4 个不同的 key 及其对应的子节点指针。一共占用 40(4*1 + 4*8)bytes。有效指针个数小于等于 4 时,使用这种类型的节点存储如下:
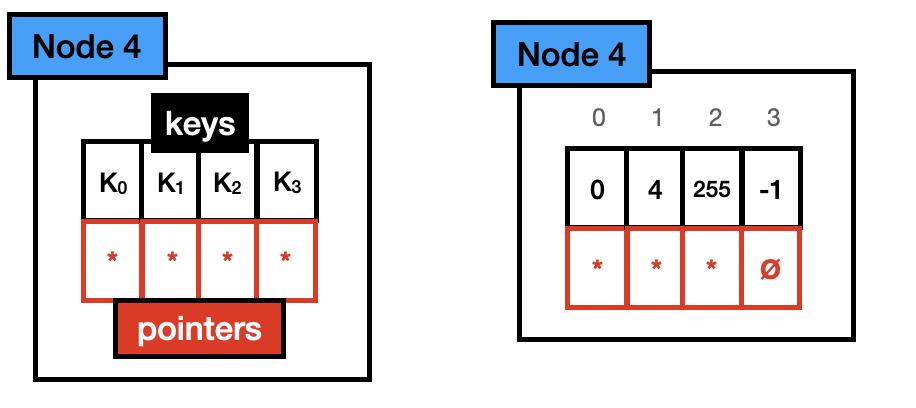
查找时,需要遍历 byte 数组,判断当前要查找的 key 是否在数组中。由于数据长度小,遍历的开销也就很低。
Node16,由一个长度为 16 的 byte 数组和长度为 16 的指针数组构成,最多存储 16 个不同的 key 及其对应的子节点指针。一共占用 144(16*1 + 16*8)bytes。有效指针个数在 5~16 时,使用这种类型的节点存储,如下:
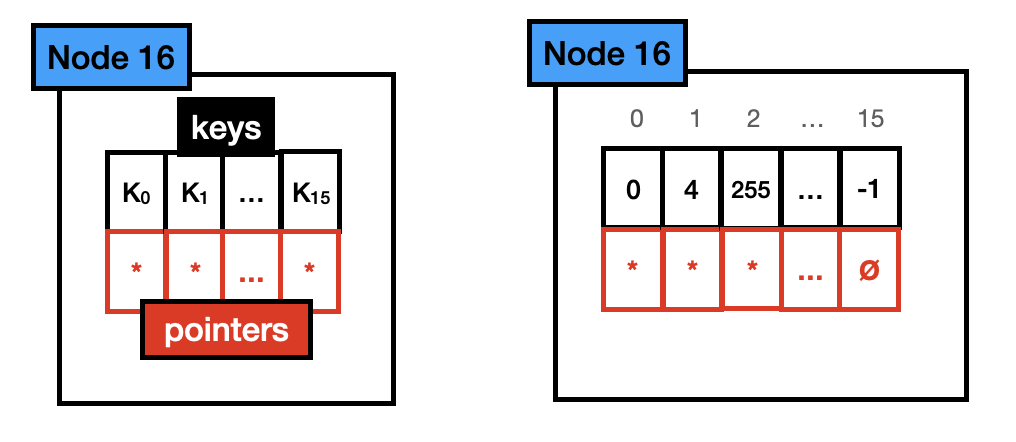
节点查找流程和 Node4 相同。
Node48,由一个长度为 256 的 byte 数组和长度为 48 的指针数组构成,最多存储 48 个不同的 key 及其对应的子节点指针。一共占用 640(256*1 + 48*8)bytes。有效指针个数在 17~48 时,使用这种类型的节点存储,如下:
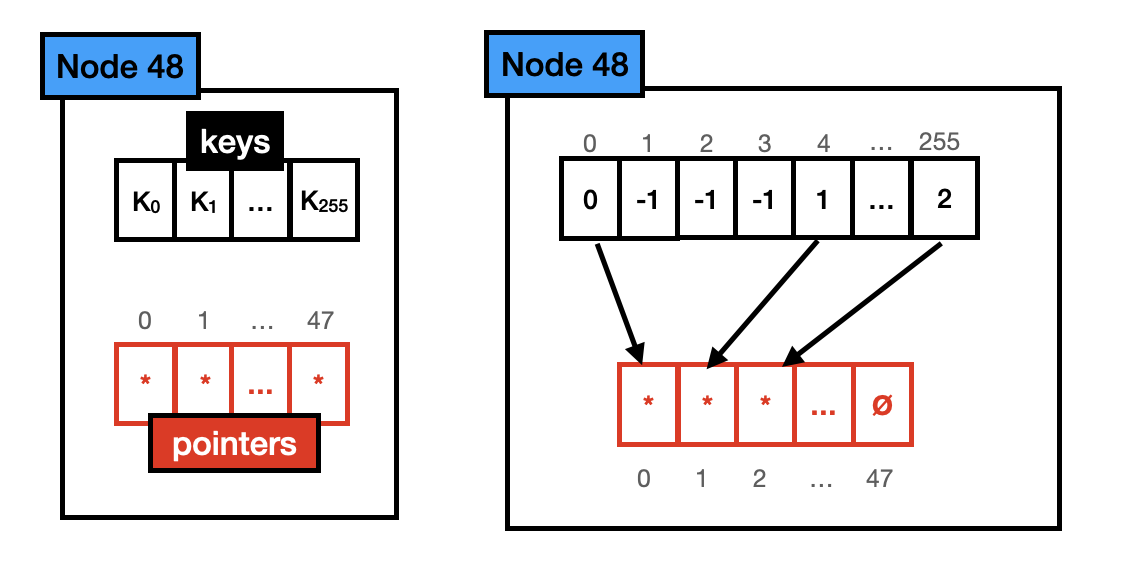
由于 byte 数组和指针数组长度不对齐,需要通过一定的方式将它们映射起来:byte 数组的下标表示 key,值表示 key 对应的子节点指针在指针数组的位置。
那么为什么 Node48 不和 Node4、Node16 保持一样的设计呢?论文中给出了解释:随着节点中元素个数的增加,遍历查找 key 数组的开销越来越大,元素个数超过 16 后,存储方式便按 Node48 存储。
我们来看下 Node48 的查找过程,查找 Node48 时,我们可以跟据查找的 key 快速定位到其在节点中的位置(key的值便是下标值),获取其对应的子节点指针。时间复杂多为 O(1),这是典型的空间换时间做法。
Node256,由长度为 256 的指针数组构成,一共占用 2048(256 * 8)bytes。有效指针个数在 49~256 时,使用这种类型的节点存储,如下:
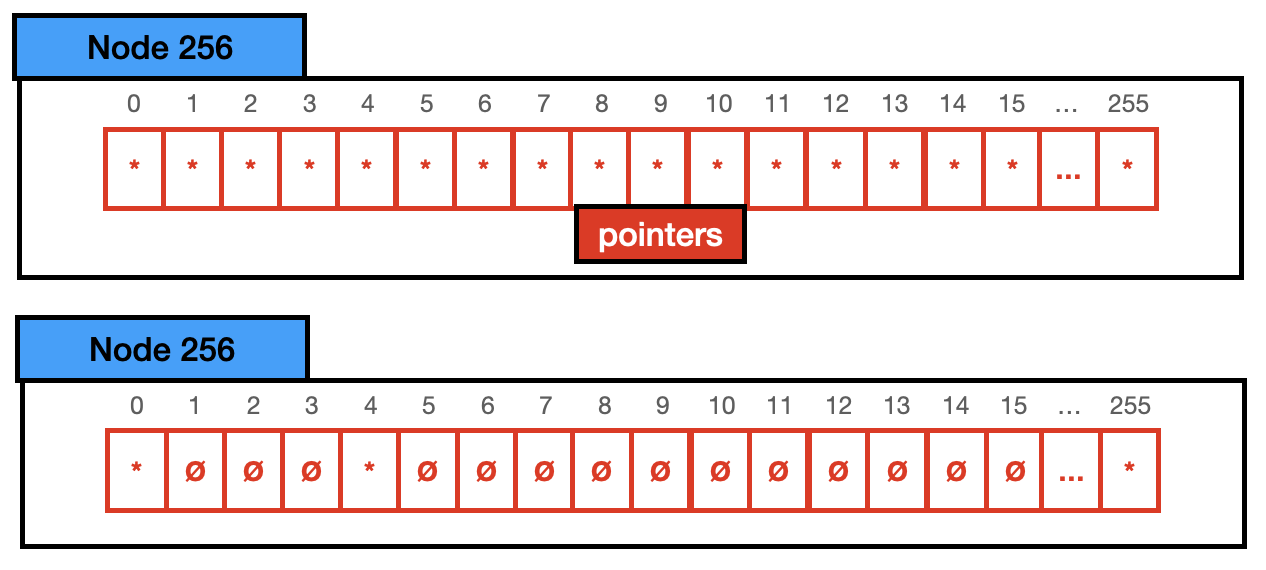
指针数组的下标代表 key,值代表其对应的子节点指针。查找是,可以快速得到子节点指针,时间复杂度为 O(1)。
因此对于前面的例子,则选取 Node4 存储,如下:
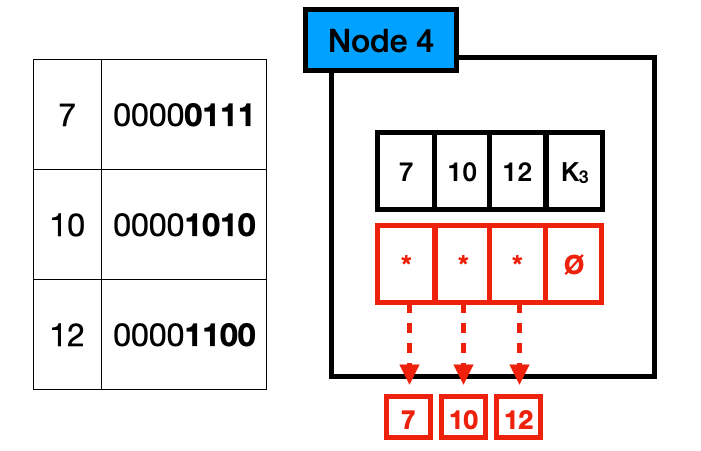
节点有一个空指针,浪费 8 bytes,比起用 Node256 来存储浪费 2024 bytes,已经减少了大量空间浪费。
Comparison
数据库常用的索引结构有 Hash 索引、B+ Tree 等,那么 ART 对比这些索引有什么优势呢?
ART 通过路径压缩、自适应节点分配极大的减少了空间浪费。相比 B+ Tree,其内部节点更小,占用空间更少,更适合 cpu cache,在纯内存场景,ART 优势明显。同时 ART 也拥有极佳的点查性能(最坏情况为 O(k)),也更适合前缀匹配查询。
B+ Tree 的优势在于树高度小且平衡,更适合作为传统数据库的磁盘索引。B+ Tree 能提供稳定高效的查询性能,且范围查询性能也很突出。因此作为磁盘索引,B+ Tree 更有优势。
Hash 索引常常能提供高效的点查性能,但是范围查询、前缀查询性能极差(全扫)。因此,Hash 索引常常用于加速点查,使用比较局限。
Conclusions
通过本文的介绍,我们大致了解了 Adaptive Radix Tree 的原理和优势。在实际技术选型过程中,应该充分结合系统应用场景,根据各自的优势,选取相对合适的技术才能充分发挥系统的能力。